EDA of CVS

Refer to EDA-UNH for more detailed description for each plot.

Basic Time Series Plot

Show the code

# candlestick plot

CVS_df <- as.data.frame(CVS)
CVS_df$Dates <- as.Date(rownames(CVS_df))

fig_CVS <- CVS_df %>% plot_ly(x = ~Dates, type="candlestick",
          open = ~CVS.Open, close = ~CVS.Close,
          high = ~CVS.High, low = ~CVS.Low) 
fig_CVS <- fig_CVS %>% 
  layout(title = "Basic Candlestick Chart for CVS")

fig_CVS

Lag plot

Show the code

CVS_ts <- ts(stock_df$CVS, start = c(2010,1),end = c(2023,1),
             frequency = 251)
ts_lags(CVS_ts)

Decomposed times series

Show the code

decompose_CVS <- decompose(CVS_ts,'additive')
autoplot(decompose_CVS)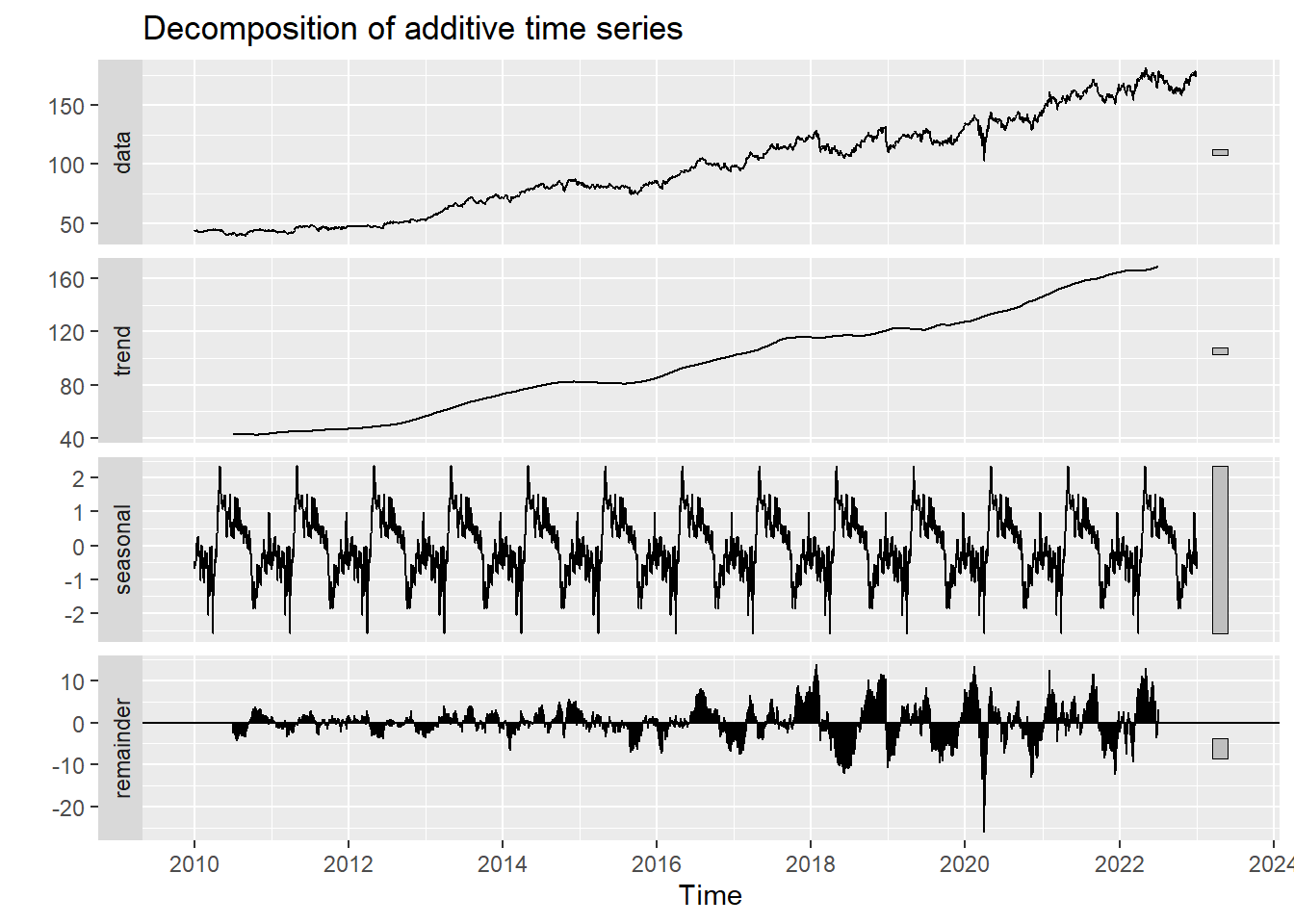

Autocorrelation in Time Series

Show the code

CVS_acf <- ggAcf(CVS_ts,100)+ggtitle("ACF Plot for CVS")
CVS_pacf<- ggPacf(CVS_ts)+ggtitle("PACF Plot for CVS")

grid.arrange(CVS_acf, CVS_pacf,nrow=2)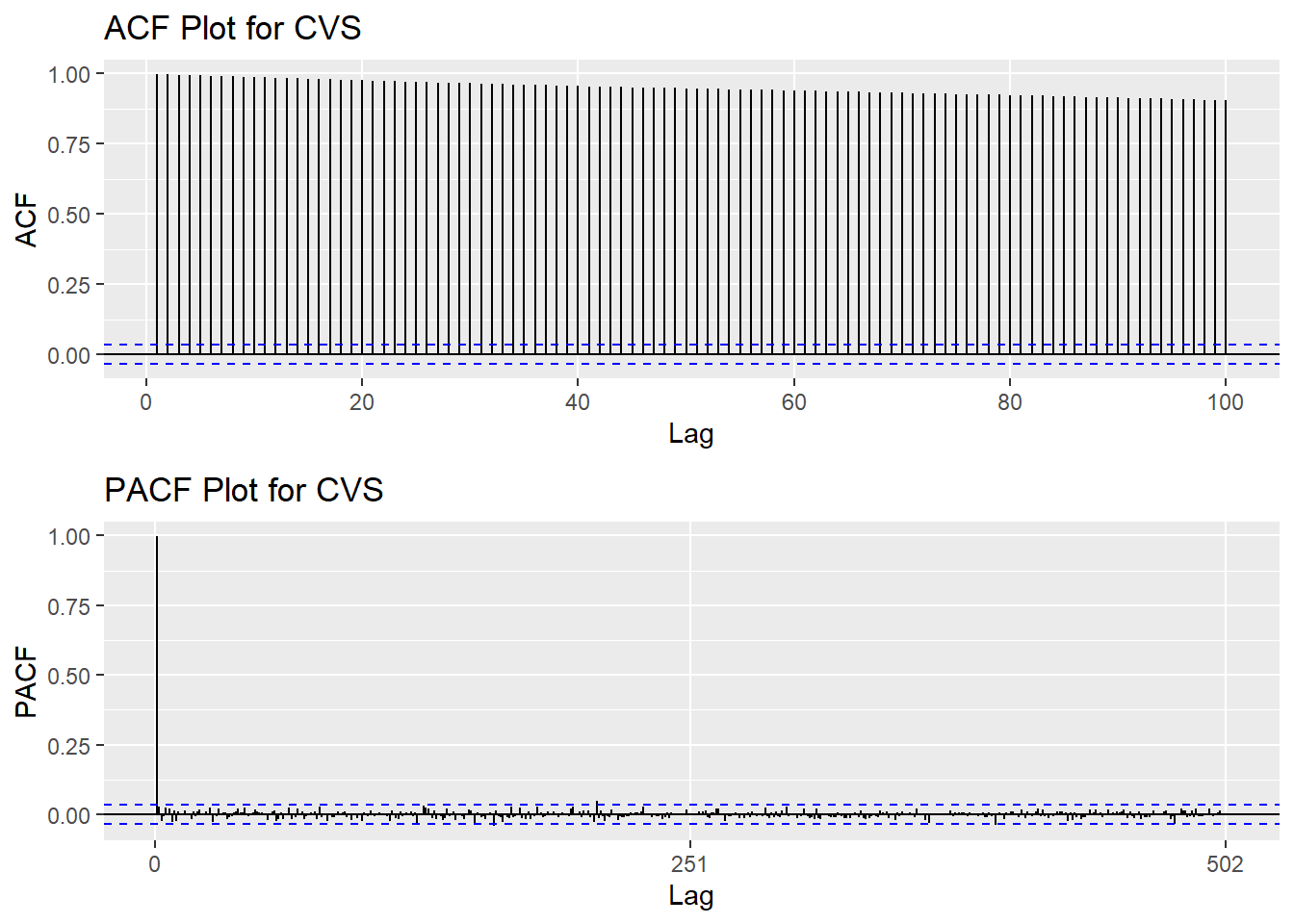

Augmented Dickey-Fuller Test

Show the code

tseries::adf.test(CVS_ts)

Warning in tseries::adf.test(CVS_ts): p-value smaller than printed p-value

    Augmented Dickey-Fuller Test

data:  CVS_ts
Dickey-Fuller = -4.5012, Lag order = 14, p-value = 0.01
alternative hypothesis: stationary

Detrending

Show the code

fit = lm(CVS_ts~time(CVS_ts), na.action=NULL) 

y= CVS_ts
x=time(CVS_ts)
DD<-data.frame(x,y)
ggp <- ggplot(DD, aes(x, y)) +           
  geom_line()

ggp <- ggp +                                     
  stat_smooth(method = "lm",
              formula = y ~ x,
              geom = "smooth") +ggtitle("CVS Stock Price")+ylab("Price")

plot1<-autoplot(resid(fit), main="detrended") 
plot2<-autoplot(diff(CVS_ts), main="first difference") 


grid.arrange(ggp, plot1, plot2,nrow=3)

Don't know how to automatically pick scale for object of type <ts>. Defaulting
to continuous.
Don't know how to automatically pick scale for object of type <ts>. Defaulting
to continuous.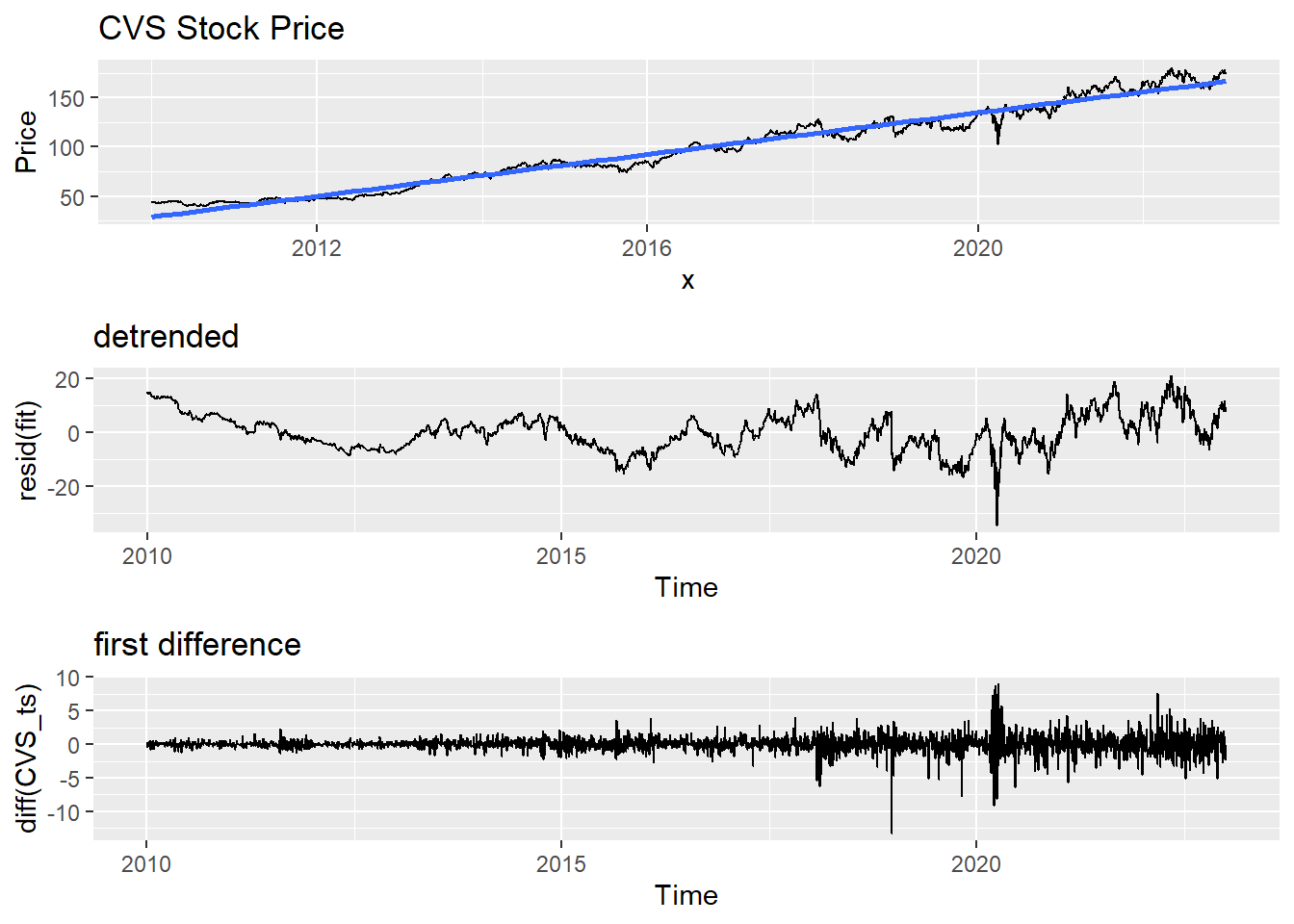

Moving Average Smoothing

Smoothing methods are a family of forecasting methods that average values over multiple periods in order to reduce the noise and uncover patterns in the data. It is useful as a data preparation technique as it can reduce the random variation in the observations and better expose the structure of the underlying causal processes. We call this an m-MA, meaning a moving average of order m.

Show the code

MA_7 <- autoplot(CVS_ts, series="Data") +
        autolayer(ma(CVS_ts,7), series="7-MA") +
        xlab("Year") + ylab("Adjusted Closing Price") +
        ggtitle("CVS Stock Price Trend in (7-days Moving Average)") +
        scale_colour_manual(values=c("CVS_ts"="grey50","7-MA"="red"),
                            breaks=c("CVS_ts","7-MA"))

MA_30 <- autoplot(CVS_ts, series="Data") +
        autolayer(ma(CVS_ts,30), series="30-MA") +
        xlab("Year") + ylab("Adjusted Closing Price") +
        ggtitle("CVS Stock Price Trend in (30-days Moving Average)") +
        scale_colour_manual(values=c("CVS_ts"="grey50","30-MA"="red"),
                            breaks=c("CVS_ts","30-MA"))

MA_251 <- autoplot(CVS_ts, series="Data") +
        autolayer(ma(CVS_ts,251), series="251-MA") +
        xlab("Year") + ylab("Adjusted Closing Price") +
        ggtitle("CVS Stock Price Trend in (251-days Moving Average)") +
        scale_colour_manual(values=c("CVS_ts"="grey50","251-MA"="red"),
                            breaks=c("CVS_ts","251-MA"))

grid.arrange(MA_7, MA_30, MA_251, ncol=1)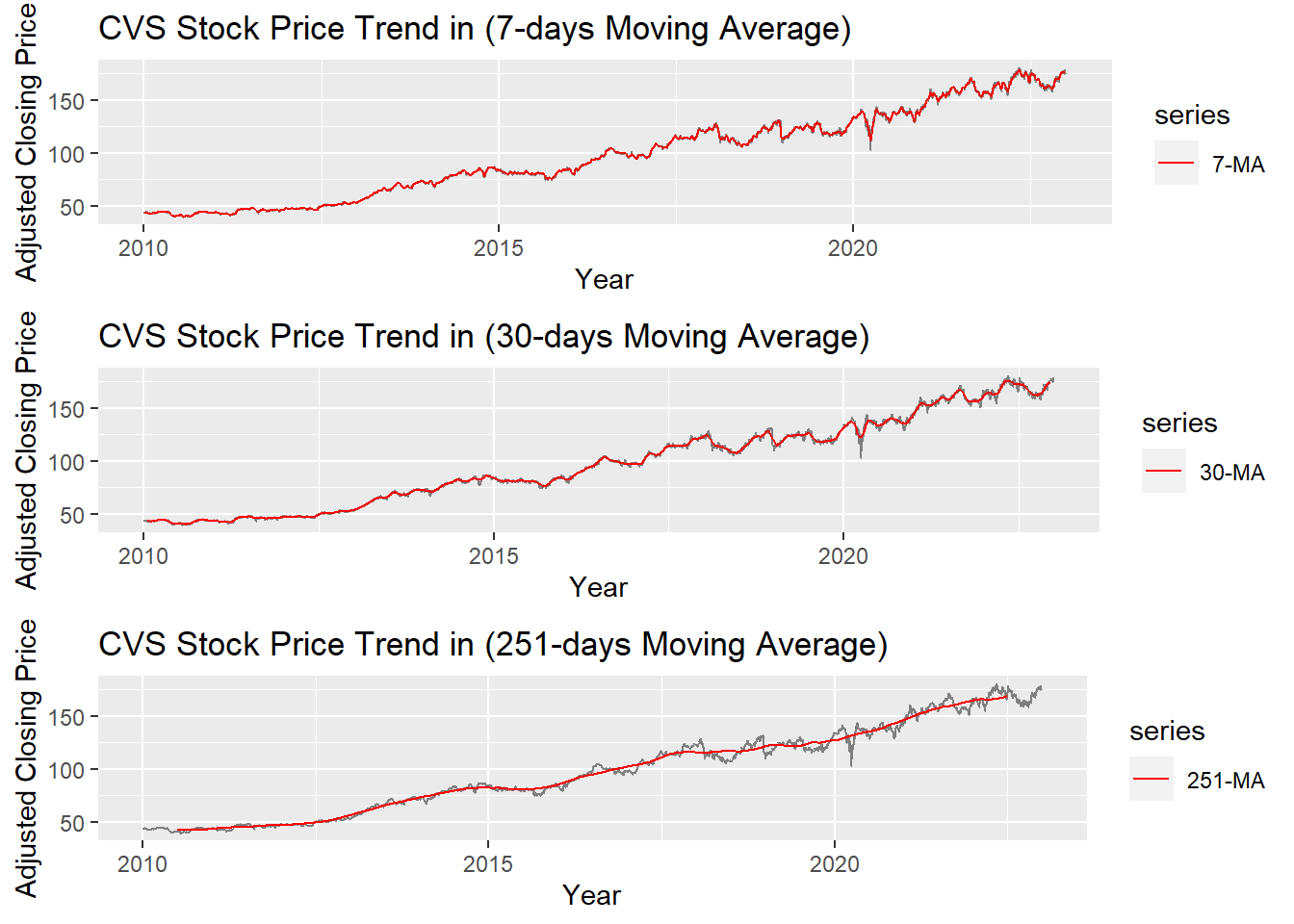

The graph above shows the moving average of 7 days, 30 days and 251 days. 251 days was choose because there are around 251 days of stock price data per year. According to the plots, it can be observed that When MA is very large(MA=251), some parts of smoothing line(red) do not fit the real stock price line. While When MA is small(MA=7), the smoothing line(red) fits the real price line. MA-30 greatly fits the real price line. Therefore, MA-30 might be a good parameter for smoothing.